Question

28 Points - The radius of a cylinder is increased by N% and its height increased by 2N%.

How does this effect the volume of the cylinder?

Let N = 20. Determine the percent increase or decrease of its volume.

Suppose the radius is decreased by 5% and the height increased by 5%. How does this effect the volume?

Answer 1

Let r be the radius of cylinder and h be the height of cylinder. If the radius of a cylinder is increased by N%, then it becomes
`R=r+(N)/(100) r`. If its height increased by 2N%, then it becomes
`H=h+(2N)/(100) h`.

The volume of initial cylinder is
`V_(initial)=\pi r^2h` and the volume of new cylinder is
`V_(new)=\pi R^2H=\pi \left(r+(N)/(100) r\right)\cdot \left(h+(2N)/(100)h\right)=\pi r^2h \left(1+(N)/(100) \right) \left(1+(2N)/(100) \right)`.

The ratio between volumes is

`(V_(new))/(V_(initial))=(\pi r^2 h\left(1+(N)/(100) \right) \left(1+(2N)/(100) \right))/(\pi r^2 h) = \left(1+(N)/(100) \right) \left(1+(2N)/(100) \right)`.

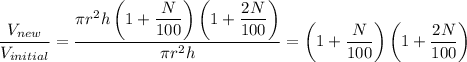This means that volume increases
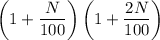`\left(1+(N)/(100) \right) \left(1+(2N)/(100) \right)` times.

1. When N=20, substitute this value into previous expression:

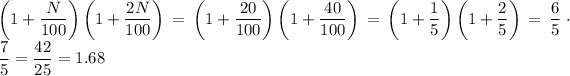`\left(1+(N)/(100) \right) \left(1+(2N)/(100) \right)=\left(1+(20)/(100) \right) \left(1+(40)/(100) \right)=\left(1+(1)/(5) \right) \left(1+(2)/(5) \right)=(6)/(5) \cdot (7)/(5) =(42)/(25) =1.68`. The coeeficient 1.68 in percent is 168% and this means that volume increases by 68%.

2. When the radius is decreased by 5%, then in first brackets you should subtract fraction and the height increased by 5%, then in secondt brackets you should add fraction. So,

`\left(1-(N)/(100) \right) \left(1+(N)/(100) \right)=\left(1-(5)/(100) \right) \left(1+(5)/(100) \right) =\left(1-(1)/(20) \right) \left(1+(1)/(20) \right) =(19)/(20)\cdot (21)/(20)=(399)/(400)=0.9975`.

The coeeficient 0.9975 in percent is 99.75% and this means that volume decreases by 0.25%.