Question

a hot air balloon is at a height of 2,250 feet. it descends 150 ft each minute. find its high after 6, 8, and 10 minutes

Answer 1

So for this, since the rate is linear we will be using the slope-intercept form, which is y=mx+b (m = slope/rate of change, b = y-intercept)

Since the rate of change "descends 150 ft per min", the m variable is -150.

The y-intercept is, in this case, the height of the balloon at 0 mins, or the starting height. Since the balloon "is at a height of 2250 ft", the b variable is 2250.

Putting our equation together, its y = -150x + 2250.

Since time is our independent variable, plug in 6, 8, and 10 mins into the x variable to solve for their heights:

`y=-150(6)+2250\\ y=-900+2250\\ y=1350\\ \\ y=-150(8)+2250\\ y=-1200+2250\\ y=1050\\ \\ y=-150(10)+2250\\ y=-1500+2250\\ y=750`

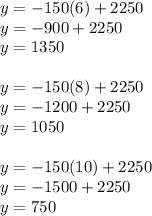
In context, after 6 minutes the balloon is at 1,350 ft, after 8 minutes the balloon is at 1,050 ft, and after 10 minutes the balloon is at 750 ft.