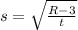Question

Solve the equation or formula for the indicated variable.


`R = ts^2 +3`

See attached pic for answers

Answer 1

subtract 3 both sides first. R-3=ts²

next, divide both sides by t, (R-3)/t=s²

finally, take the square root of both sides

√(R-3)/t = s. 2nd choice.

Answer 2

The correct answer is the second option:
`s=\sqrt{(R-3)/(t)}`

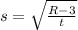
Explanation:

The idea is to get the variable
`s` for alone on one side. To do that follows the following steps:

1. Pass the number
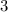`3` to subtract to the left.

`R=t\cdot s^2+3`

`R-3=t\cdot s^2`

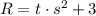
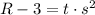
2. Pass the letter
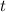`t` to divide to the left side.

`(R-3)/(t)=s^2`

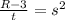
3. Take the squared root on both sides.

`\sqrt{(R-3)/(t)}=√(s^2)`

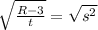
4. The right part can be simplified to
`s` because the power and the root are canceled.

`\sqrt{(R-3)/(t)}=s`

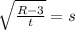
5. The solution of the equations is:

`s=\sqrt{(R-3)/(t)}`

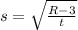
Thus, the correct answer is the second option:
`s=\sqrt{(R-3)/(t)}`