Question

The radioactive substance uranium-240 has a half-life of 14 hours. The amount

A(t) of a sample of uranium-240 remaining (in grams) after t hours is given by the following exponential function.
At = 3900(1/2) t/14
Find the initial amount in the sample and the amount remaining after 40 hours.
Round your answers to the nearest gram as necessary.

PLEASE HELP ASAP

Answer 1

To solve this problem, we just need to substitute the right value for the variable time.

The given expression is

`A(t)=3900((1)/(2) )^{(t)/(14) }`

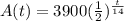
Where the initial condition is determined when
`t=0`.

`A(t)=3900((1)/(2) )^{(0)/(14) }=3900(1)=3900`

Therefore, the initial amount is 3900 grams.

Then, after 40 hours refers to
`t=40`

`A(t)=3900((1)/(2) )^{(40)/(14) } \approx 538.24`

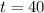
Therefore, after 40 hours, there's 538.24 grams remaining, approximately.

Answer 2

we are given

`A(t)=3900((1)/(2))^{(t)/(14)}`

(a)

For finding initial amount , we can set t=0

and find A(t)

`A(0)=3900((1)/(2))^{(0)/(14)}`

`A(0)=3900((1)/(2))^(0)`

`A(0)=3900`

so, initial amount is 3900 grams..........Answer

(b)

We can plug t=40

and find A(t)

`A(40)=3900((1)/(2))^{(40)/(14)}`

`A(40)=538`

so, the amount remaining after 40 hours is 538 grams...........Answer