Question

Determine if the graph is symmetric about the x-axis, the y-axis, or the origin. r=-3-2 cos(theta)

Answer 1

Yes

Explanation:

Since, it is a graph in polar coordinates, So we can start with the base equation of this given equation which should be:

`r = cos(theta)`

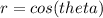
and its graph is a circle with centre at (0.5,0), if we multiply it by 2, then its radius will be doubled and it will become:

`r =2 cos(theta)`

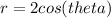
Thus, giving a circle of radius 1. If we multiply it by -1, then:

`r =-2 cos(theta)`

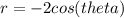
It will give us a circle shifted 1 units to the left. If we add 3 in it, we will get a cardioid which is passing through y = 3 and y = -3 at x = 0,

`r =3-2 cos(theta)`

And this graph will be a symmetric graph about the x-axis. Hence the answer is Yes.

Answer 2

now, let's keep in mind that cos(π) = -1, and that sin(π) = 0, thus cos(π)cos(θ) is just -cos(θ), and sin(π)sin(θ) is just 0sin(θ) or just 0.

Also let's recall that symmetry identity of cos(-θ) = cos(θ).

`image`

`image`