There are a number of ways you can solve this using elmination. The basic idea is to multiply one or both of the equations by something so that the coefficients of one of the variables is the same or opposite in the two resulting equations.
Here, this could mean you multiply the second equation by 2 to make the y-coefficient -2, which is the opposite of the y-coefficient in the first equation, 2.
I like better the idea of dividing the first equation by 2. This also makes the y-coefficient the opposite of its value in the second equation. Now, your equations are
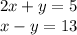
Adding these two equations gives

The second equation can be rearranged to tell you
... y = x - 13
so, for x=6, this gives
... y = 6 - 13 = -7
Your solution is (x, y) = (6, -7).
_____
Since we used the second equation to get the value of y from x, we know these values satisfy that one. We can check them in the first equation:
... 4·6 + 2·(-7) = 24 - 14 = 10 . . . . . values also satisfy the first equation