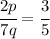Question

Given that (4p-5q)/(6p+q) = 1/4 , find the value of 2p : 7q in its lowest term.

Answer 1

Start from

`\cfrac{4p-5q}{6p+q} = \cfrac{1}{4}`

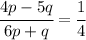
and cross multiply the denominators (i.e. multiply both sides by
`4(6p+q)`

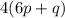
The result is

`4(4p-5q) = 6p+q`

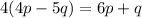
Expand the left hand side:

`16p-20q = 6p+q`

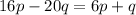
Bring all terms involving p to the left, and all terms involving q to the right:

`16p-6p = 20q+q \implies 10p=21q`

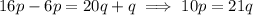
Divide both sides by 21q:

`\cfrac{10p}{21q} = 1`

Now we have a ratio between multiples of p and q. It's not exactly the one we want, though. Nevertheless, we can keep multiplying both sides by approriate constants in order to get the ratio we want:

Divide both sides by 5:

`\cfrac{2p}{21q} = \cfrac{1}{5}`

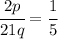
Multiply both sides by 3:

`\cfrac{2p}{7q} = \cfrac{3}{5}`

Answer 2

`image`