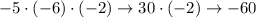Question

Evaluate this expression: [(5-5)^2 - 15 ÷ 3] • -6 • -2

I need help because I’m not sure how to solve with these [ ] symbols

Answer 1

The square brackets are just another type of brackets. They work exactly as round brackets, and we only use them for aesthetic reasons: these two expressions are absolutely equivalent:

`[(5-5)^2 - 15 / 3] \cdot (-6) \cdot (-2)`

and

`((5-5)^2 - 15 / 3) \cdot (-6) \cdot (-2)`

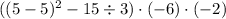
As for how to solve it, you perform operations inside parentheses first, going inside out (so inner parentheses first), and the other operations follow the same order.

So, first of all, we compute the innermost round parenthesis:

`[(5-5)^2 - 15 / 3] \cdot (-6) \cdot (-2) \to [0^2 - 15 / 3] \cdot (-6) \cdot (-2)`

Now we have the square brackets. So, we perform the operations inside them: exponents first, but 0^2 is still 0, so we have

`[0^2 - 15 / 3] \cdot (-6) \cdot (-2) \to [0 - 15 / 3] \cdot (-6) \cdot (-2)`

Still inside square brackets, divisions next:

`[0 - 15 / 3] \cdot (-6) \cdot (-2) \to [0 - 5] \cdot (-6) \cdot (-2)`

Now we can compute the bracket:

`[0 - 5] \cdot (-6) \cdot (-2) \to -5 \cdot (-6) \cdot (-2)`

Now we're left with multiplications only. They're commutative, so we can perform them in any order. We have

`-5 \cdot (-6) \cdot (-2) \to 30 \cdot (-2) \to -60`

Answer 2

[(5-5)^2-15/3]•-6•-2

[0^2-15/3](-6)(-2)

[0-5](-6)(-2)

[(-5)(-6)](-2)

30•-2

ANSWER:-60