Answer:
Option C.
Explanation:
Given information: Line PA and PB tangent to the circle,
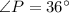 .
.
Draw the radius from the point A and B.
The tangent to a circle is perpendicular to the radius at the point of tangency.
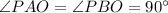
OAPB is a quadrilateral and the sum of all interior angles of a quadrilateral is 360°.
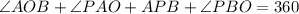
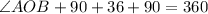
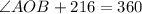
Subtract 216 from both sides.
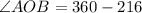
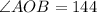
The measure of arc AB is 144°.
Therefore, the correct option is C.