Question

Use properties of limits to find the indicated limit. It may be necessary to rewrite an expression before limit properties can be applied.

limx→1 x3+5x2+3x−9x−1

Answer 1

The limit of the given function : x³ + 5x² + 3x - 9x - 1 is -1

Explanation:

The polynomial function for which we need to calculate the limit is given to be : x³ + 5x² + 3x - 9x - 1

`\lim_(x \to 1) x^3+5x^2+3x-9x-1`

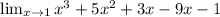
Now, since it is a polynomial function so the limit always exist for this function. Hence, we can directly substitute the value of x = 1 in the function and can find the resultant limit for the given function.

`\lim_(x \to 1) x^3+5x^2+3x-9x-1\\\\\implies 1^3+5* 1^2+3* 1-9* 1-1\\\\\implies 1 + 5+3-9-1\\\\\implies -1`

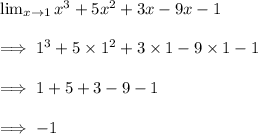
Therefore, The limit of the given function : x³ + 5x² + 3x - 9x - 1 is -1