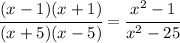Question

What is the product of the rational expression

Answer 1

The equations are what’s known as “completing the squares,” which basically means that when you multiply it out, the middle cancels out

(x - 1)(x + 1)/(x + 5)(x - 5)
x^2 - x + x - 1/x^2 + 5x - 5x - 25
x^2 - 1/x^2 - 25

The answer is C

Answer 2

Multiplying two fractions is very easy: you need to multiply one numerator with the other, and one denominator with the other.

So, in your case, the answer is

`\cfrac{x-1}{x+5} \cdot \cfrac{x+1}{x-5} = \cfrac{(x-1)(x+1)}{(x+5)(x-5)}`

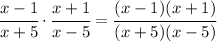
Both expressions at numerator and denominator are in the form
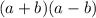`(a+b)(a-b)`. This is a known case, where the result is the difference of the squares:

`(a+b)(a-b) = a^2-b^2`

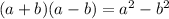
So, the answer is

`\cfrac{(x-1)(x+1)}{(x+5)(x-5)} = \cfrac{x^2-1}{x^2-25}`