LCM stands for least common multiple, and so the LCM of two number is the smallest possible common multiple of the two numbers.
Since 16 is already a multiple of 8 (and since every number is a multiple of itself), the LCM between 8 and 16 is sixteen itself: it is a multiple of 8, it is a multiple of 16, and there couldn't be a smaller one.
Even though this case was trivial, let's do the computation to learn how to do this in general: first of all, you need the prime factorizations of the two numbers:
The LCM of the two numbers is composed by all the primes appearing in any of the two factorizations. In case a prime appears in both factorizations, we choose the one with higher exponents.
In this case, 2 is the only prime to appear in both factorizations. So, we choose the one with higher exponent, which is 4, and the answer is
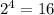, as we already observed.