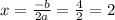Answer:
y = x^2 + 2
Explanation:
find the equation below whose axis of symmetry is x = 0
to find axis of symmetry we use formula x= -b/2a
WE compare the equation with the form y =ax^2 + bx+c
y = x^2 + 2x
a= 1 and b = 2 so
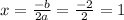
y = x^2 − 16x + 58
a= 1 and b = -16 so
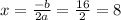
y = x^2 + 2
a= 1 and b = 0 so
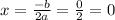
y = x^2 − 4x + 2
a= 1 and b = -4 so