Area a(w)=
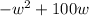 where w is the width
where w is the width
Area is in quadratic form.
To find maximum are we need to find the vertex.
a(w)=
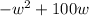
To find vertex we use formula w=
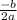
a= -1 and b = 100
So w =
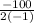 = 50
= 50
We will get maximum area when width w= 50m
To find maximum are we plug in 50 for w and find a(50)
a(w)=
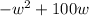
a(50)=
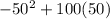
a(50)= -2500 + 5000
= 2500
So maximum area is 2500 square meter and the dimensions are length = 50m , width = 50m