Question

How to find the least common multiple in a number

Answer 1

Well, there are a few ways.

The easiest would be to factor the two(or more) numbers you want to find the LCM of and only consier the prime factor with the highest degree. An example of this is if you wanted to find the least common multiple of 30 and 28, you first factor them:

`30=2*5*3\\28=7*2^2`

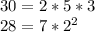
So then you only consider the highest factors between them:

`lcm(30,28)=2^2*7*3*5=420`

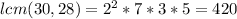
Another way of doing it is:

`\text{lcm}}(30,28)=\frac{30*28}{\gcd{(30*28)}}`

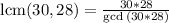
This is essentially the same as the step above, but it requires (I feel) more steps and thinking. It works because when you multiply 30 and 28, you actually "overcount" their factors in a sense. That's because you multiply the numbers they share, like 4 and 2, instead of just considering the 4. When you divide by the greatest common divisor between the two, you account for this by removing any factor they share. So now you only consider the highest between the two, which is what we want. The second method works for numbers that are too big to reasonably factor. You can use the Euclidean algorithm to make finding the GCD much easier than it would be to find the factors. Either way works though.

Answer 2

Multiply each factor the greatest number of times it occurs in any of the numbers. 4 has two 2s, and 18 has one 9, so we multiply 2 two times, and 9 once. This gives us 36, the smallest number that can be divided evenly by 2, 4, and 18.