Question

A circular garden has a circumference of


`( {8xy}^(2)\pi)`
What is the length of a straight path that goes through the centre of the garden?

What is the area of the garden?

Answer 1

This solution to this problem is predicated on the fact that the circumference is just:
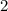`2\pir`. A straight line going through the center of the garden would actually be the diameter, which is well known to be two times the radius of the circle, so we can say that the circumference is just:

`d\pi`

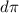
So, solving for both the radius and the diameter gives us:

`image`

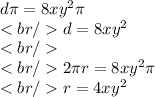
So, the length of thes traight path that goes through the center of the guardain is just
`8xy^2`, and we can use the radius for the next part of the problem.

The area of a circle is
`\pi r^2`, which means we can just plug in the radius and find our area:

`image`

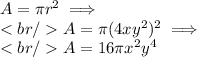
So, we have found our area(
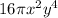`16 \pi x^2 y^4`) and the problem is done.