Question

Find the island height of a pyramid with a volume of 432 ft^3 if the base is a square with a side length of 12 ft. Round to the nearest tenth.

I would appreciate some help with this question as I don't fully understand what it's asking, abit of an explanation would be appreciated too!

Answer 1

So the picture below shows what the slant height is. It also shows that the pyramid can form a right triangle, in which we can use the pythagorean theorem, which is
`leg^2+leg^2=hypotenuse^2` .

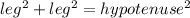But first, we have to find the height of this pyramid. The volume formula for a square pyramid is
`A=(lwh)/(3)` . Since we know its a square pyramid, the length and width are going to be the same (12 ft), and we know that the volume is 432 ft^3. Using this info, we can solve for the height:

`432=(12*12*h)/(3)\\ 1296=12*12*h\\ 1296=144*h\\ 9=h`

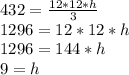
So now we can use the pythagorean theorem (remember to split the 12 by 2, since the right triangle has only half the length of the base). Our equation will be solved as such:

`6^2+9^2=s^2\\ 36+81=s^2\\ 117=s^2\\ 10.8=s`

In short, the slant height is 10.8 ft.