So, we know that a quadratic equation is always reflected over its axis of symmetry. Using that fact, we can actually find the vertex of the quadratic without having to foil!
So, our first step is to find the distance between the roots. We know that the function intersects the x axis at (2,0) and (8,0), which tells us that the distance between the roots is 6 units. Because the axis of symmetry makes the distance between the x value of the vertex and the two roots uniform, that means we should divide this by two to get the aforementioned value. So we have the distance from the x value of the vertex to either root to be 0. At this point we can either subtract 3 from 8 or add 3 to 2 to give us an x value of 5 for the vertex.
The next part is super easy. Since we know the x value is 5, we just have to find f(5) which is just:
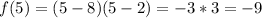
So we know our y value is -9, and with that we can deduce that our vertex is at (5,-9)