Question

The second term of the expansion (3x-4y)^5 is

Answer 1

To solve this, we're going to have to use the binomial theorem. It states that:

`(x+y)^(n)=\sum_(k=0)^(n) \binom{n}{k}x^(n-k)y^k`

If you want a specific term, we can just disregard the polynomial and use this:

`A_k= \binom{n}{k-1}x^(n-k-1)y^(k-1)`

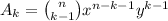
Where A_k is the kth term. In the context of this problem it would look like:

`A_2= \binom{5}{1}(3x)^(5-1)(-4y)^1= 5*81*-4*x^4*y=1620x^4y`

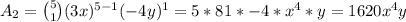
So, based on that, our second term is
`1620x^4y`