6.
So for this, since the circle is open, you are going to be replacing x in g(x) with -4x + 1. It will be solved as such:
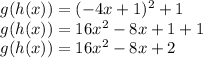
8.
So firstly, we will need to solve g(f(x)) before we can do h(g(f(x))). So replace x in g(x) with x - 3:
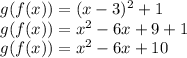
So now that we know what g(f(x)) is, we can solve for h(g(f(x))). To do this, replace x in h(x) with x^2 - 6x + 10:
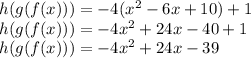
In short, h(g(f(x))) = -4x^2 + 24x - 39.