Question

Which rational number equals 0 point 3 with bar over 3?

Answer 1

0.333.. repeating =
`(1)/(3)`

Explanation:

The given number is 0.333...

The bar represents 3 continues forever.

Let's find the rational number that represents 0.333...

The rational number is in the form of
`(p)/(q)`, where q ≠ 0.

Let x = 0.333...

Let's multiply both sides by 10, we get

10x = 3.33...

Now let's subtract x from 10x

10x - x = 3.33... - 0.333..

9x = 3

Now let's divide both sides by 9, we get

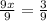
`(9x)/(9) = (3)/(9)`

x =
`(3)/(9)`

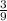
When we simplify the above, we get

x =
`(1)/(3)`

So the rational number
`(1)/(3)` represents 0.333....

Answer 2

The overbar indicates the digit repeats forever. It is worth remembering that

`0.\overline{x}=(x)/(9)\qquad\text{x = any single digit}`

Your number is 3/9 = 1/3