With a standard form quadratic, we see that with the quadratic formula:
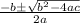
That the part under the radical (
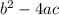 ) can tell us many things about how the roots of this polynomial behave.
) can tell us many things about how the roots of this polynomial behave.
If b^2-4ac were 0, that would mean the polynomial would have one root at
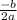 . We call that a double root at (-b/2a,0).
. We call that a double root at (-b/2a,0).
If the discriminant is a perfect square, we note that the radical can be reduced and this the fraction is a rational number.
If the discriminant is negative, it means it has no real roots. That's because the root of a negative number is imaginary.
The last case if is the discriminant is neither a negative or a perfect square. That means the radical cannot be reduced and we will have two irrational roots.
In this problem, we see that the discriminant is:
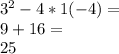
The answer to the problem you asked is then 25, and we can also note that this quadratic has real, rational roots.