Question

The distance of an object thrown upward is modeled by the equation h=-2x^2+3t+4, where h is the height of the object in feet at any given time and t is the time in seconds. The object is visible whenever it is at h (greater than or equal to) 0. For how long is the object visible?

Answer 1

So for this, we will have to find the zeros (x-intercepts) of the equation. In this case, we will be using the quadratic formula, which is
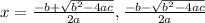`x=(-b+√(b^2-4ac))/(2a),(-b-√(b^2-4ac))/(2a)` (a = x^2 coefficient, b = x coefficient, c = constant). Using our info, our equation is such:
`x=(-3+√(3^2-4*(-16)*4))/(2*(-16)),(-3-√(3^2-4*(-16)*4))/(2*(-16))`

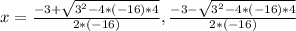
Firstly, solve the multiplications and the exponents:
`x=(-3+√(9+256))/(-32),(-3-√(9+256))/(-32)`

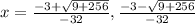
Next, do the addition:
`x=(-3+√(265))/(-32),(-3-√(265))/(-32)`

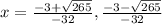
Next, plug in the equations into the calculator and your answer will be:
`x=-0.41,0.60`

Since we can't have negative time in this situation, it can't be -0.41 seconds. Which means that the object is visible for about 0.60 seconds, or C.