Question

X and y are positive integers. explain why incorrect to claim that


`(x )/( √(y) )`
is always irrational

Answer 1

You can find counterexamples to disprove this claim. We have positive integers that are perfect square numbers; when we take the square root of those numbers, we get an integer.

For example, the square root of 1 is 1, which is an integer. So if y = 1, then the denominator becomes an integer and thus we get a quotient of two integers (since x is also defined to be an integer), the definition of a rational number.

Example: x = 2, y = 1 ends up with
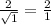`(2)/(√(1)) = (2)/(1)` which is rational. This goes against the claim that
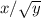`x/√(y)` is always irrational for positive integers x and y.

Any integer y that is a perfect square will work to disprove this claim, e.g. y = 1, y = 4, y= 9, y = 16. So it is not always irrational.