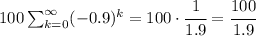Two quick changes before diving into action:
First of all, we can factor the 100 out of the sum:
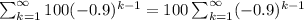
Secondly, we can see that the index k starts from 1, but the exponent is k-1. This means that when k=1, the exponent is actually 0. When k=2, the exponent is actually 1, and so on. So, we can rewrite the sum as
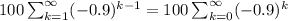
Now, let's focus on the sum. First of all, it converges, because every sum like

converges if and only if
 , which is the case because
, which is the case because
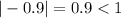
Also, in this case we have

so in your case you have

and let's not forget the 100 we factored at the beginning!