Answer:
Concave up at
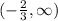
Concave down at

Explanation:
The given function is
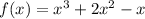
In order to check the concavity, we find the inflection point. To find inflection point we calculate the second derivative of the function and then equate it to zero.
The first derivative is given by
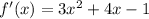
The second derivative is given by
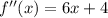
For inflection point
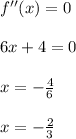
Hence, the inflection point is
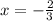
Hence, on the left of
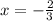 the curve is concave downward and on the right of
the curve is concave downward and on the right of
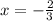 the curve is concave up.
the curve is concave up.
Hence,
Concave up at
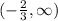
Concave down at
