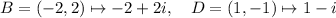On the complex plane, the number
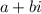 is mapped onto the point with coordinates
is mapped onto the point with coordinates
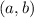 .
.
In other words, the x coordinate is the real part of the number, while the y coordinate is the complex part of the number.
Viceversa, if you start from a point
 , you can identify the number
, you can identify the number
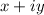 .
.
So, the endpoints of the diagonal are the points
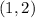 and
and
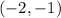 . These are points A and C in the attached figure.
. These are points A and C in the attached figure.
This means that points B and D have coordinates
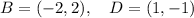
So, the correspondant complex numbers are