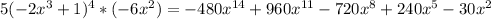To solve this problem, we're going to have to use the chain rule. Let
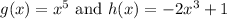
f(x)=g(h(x)) which means that g(x)'s input changes at a different speed than x and that speed is the derivative of h(x). Written down, since it seems kinda weird to explain, we have:
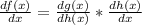
so that mean's we're analyzing:
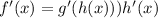
So: