Question

Assuming the conditions regarding the motion represented in the graph remain the same, determine the acceleration of the object at t=200 s.

What is the instantaneous acceleration at t= 10s

Answer 1

Option a

Explanation:

Given is the graph showing the relation between time and velocity.

Velocity is shown on y axis, time on x axis.

The graph shows that relation is linear with constant slope

To find equation we see that y intercept is 4,

Two points are (0,4) and (10,10)

Slope=
`(10-4)/(10)=0.6`

So equation for v is

v=0.6t+4

Now to find acceleration we can find derivative of v

For one unit change in t, v changes by 0.6 m

In other words, rate of change of velocity =

acceleration = 0.6 m/sec^2

Since acceleration is independent of t, we get

for t =10 s also

acceleration =0.6m/sec^2

OPtion a is right

Answer 2

(a)

We can see that

this is a straight line

and this is the graph of velocity

we know that

acceleration is the derivative of velocity

so, slope of curve of velocity is acceleration

so, we will find slope of this line

We can select any two points

(0,4) and (5,7)

we can use slope formula

`m=(y_2-y_1)/(x_2-x_1)`

now, we can plug points

`m=(7-4)/(5-0)`

`m=0.6`

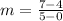
we know that slope of line is always constant irrespective of any value of t

so, acceleration will always be same irrespective of any value of t

so, we will get acceleration

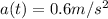`a(t)=0.6m/s^2`............Answer

(b)

we can see that acceleration is constant

and we know that

derivative of constant is always 0

so, instantaneous rate of acceleration at t=10s is 0........Answer