Answer:
The length of VZ is 10 units .
Explanation:
As given
Z is the circumcenter of triangle TUV.
By using the properties of circumcentre .
The vertices of a triangle are equidistant from the circumcenter.
Thus
VZ = UZ = TZ
As given in the figure.
UZ = 3x + 4
TZ = 5x
As UZ = TZ
3x + 4 = 5x
5x - 3x =4
2x = 4
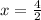
x = 2
Put x = 2 in UZ = 3x + 4 and TZ = 5x
UZ = 3 × 2+ 4
= 6 + 4
= 10 unit
TZ = 5 × 2
= 10 unit
(As VZ = UZ = TZ )
Thus VZ = 10 units
Therefore the length of VZ is 10 units .