Question

Select the graph of the equation below. please help

Answer 1

Answer with explanation:

We are given a quadratic equation as:

`y=(3)/(2)x^2-6x`

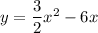
We know that the x-intercept of the graph are the points where y=0

i.e.

`(3)/(2)x^2-6x=0`

i.e.

`3x^2-12x=0`

i.e.

`3x(x-4)=0`

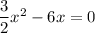
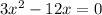
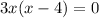
i.e. x=0 or x=4

Hence, the only graph which satisfy the x-intercept of the given quadratic equation is attached to the answer.