1 Answer

Greg Blass · Answer 1 · 2019-08-22T03:09:37+0000

True.

Let's call the sides of the two right triangles as follows:

Triangle 1: legs a,b, hypothenuse c.

Triangle 2: legs x,y, hypothenuse z.

Suppose we know that a=x and c=z. By Pythagorean theorem, we have for both triangles

$\text{hypotenuse}^2 = \text{leg}_1^2 + \text{leg}_2^2$

So, in triangle 1 we have

c^2 = a^2+b^2

while in triangle 2 we have

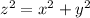
z^2 = x^2+y^2

But since a=x and c=z, the second equation becomes

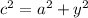
c^2 = a^2+y^2

Solve the equations for y^2 and b^2: we have in both cases

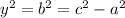
y ^2 = b^2 = c^2-a^2

This, in theory, would mean
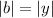|b|=|y| , but they are length of a triangle, and thus are both positive, which concludes the proof.

Please log in or register to add a comment.