Answer:
B.
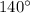
Explanation:
We have been given an image of a circle. We are asked to find the measure of arc BC.
We know that full arc measure of semicircle is 180 degrees. Since AD is diameter of our given circle, so we can set an equation to find measure of arc BC as:

Upon substituting the given measure of angles, we will get:
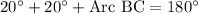
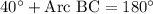
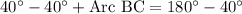
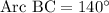
Therefore, the measure of arc BC is 140 degrees and option B is the correct choice.