We'll do this last last one real slow.
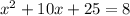
Step one, move the 8 to the left side by subtracting it from 25:
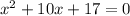
To factor we'd need factors of 17 which add to 10. The only factors of 17 are 17 and 1 so there's no factoring. We use the quadratic formula.
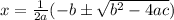
a, b and c refer to the coefficients on the quadratic equation. We have
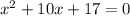 so a=1 (the coefficient on x^2) b=10, c=17.
so a=1 (the coefficient on x^2) b=10, c=17.
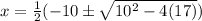
Now we simplify the square root. 10²=100, 4(17)=68, so
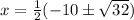
32 = 16(2) so we can simplify a bit more.

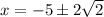
We compare to the answers and get
Answers: A E
With the Shakespeare Quadratic Formula shortcut
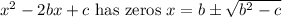
Using that on
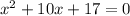 we could have gotten here a bit quicker. b=-5 this time, c=17, so
we could have gotten here a bit quicker. b=-5 this time, c=17, so
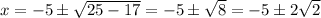
Good luck. Please ask questions if you're still unsure.