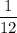Answer:
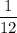
Explanation:
Given : If two balanced die are rolled, the possible outcomes can be represented as follows.
(1, 1) (2, 1) (3, 1) (4, 1) (5, 1) (6, 1) (1, 2) (2, 2) (3, 2) (4, 2) (5, 2) (6, 2) (1, 3) (2, 3) (3, 3) (4, 3) (5, 3) (6, 3) (1, 4) (2, 4) (3, 4) (4, 4) (5, 4) (6, 4) (1, 5) (2, 5) (3, 5) (4, 5) (5, 5) (6, 5) (1, 6) (2, 6) (3, 6) (4, 6) (5, 6) (6, 6)
Counting all the outcomes , the total outcomes = 36
Outcomes having um of the dice is 10 = (5, 5) (4, 6) (6, 4)
Number of outcomes having um of the dice is 10 = 3
i.e. Number of favorable outcomes = 3
We know that ,
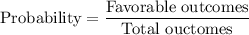
Thus, the probability that the sum of the dice is 10 =

Hence, the required probability =