Question

Throwing with the wind, a quarterback passes a football 140 ft in 2 s. against the wind, the same pass would have traveled 80 ft in 2 s. find the rate of the pass and the rate of the wind.

Answer 1

When we throw the ball along the direction of the wind then the net speed of the ball is sum of speed of ball and speed of wind.

`v = v_(ball) + v_(wind)`

`(140)/(2) = 70 ft/s = v_(ball) + v_(wind)`

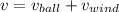
Now when wind is blowing opposite to the direction of the ball then net speed is subtraction of ball speed and wind speed

`v = v_(ball) - v_(wind)`

`(80)/(2) = 40 ft/s = v_(ball) - v_(wind)`

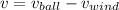
Now if we subtract above two equations

`70 - 40 = 2*v_(wind)`

`v_(wind) = 15 ft/s`

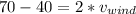
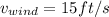
so wind speed will be 15 ft/s