we will select each options and find zeros
(a)
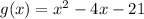
for finding x-intercept , we can set g(x)=0
and then we can solve for x
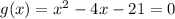
now, we can factor it

we get
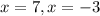
so, this is TRUE
(b)
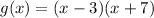
we can set it to 0
and then we can solve for x
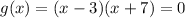
we get
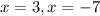
so, this is FALSE
(c)
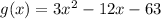
we can set it to 0
and then we can solve for x
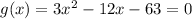
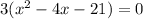

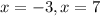
so, this is TRUE
(d)
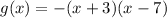
now, we can set it to 0
and then we can solve for x
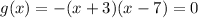
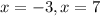
so, this is TRUE
(e)
we have

now, we can set it to 0
and then we can solve for x
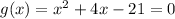
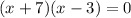
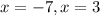
so, this is FALSE