Answer:
$129.82
Explanation:
We are given that the figure is two isosceles triangles. Both triangles have a base of 2 cm and both have legs of 5 cm.
To find the area of a triangle, we use the formula A = 1/2bh, where b is the base of the triangle and h is the height.
We do not have the height of the triangles; we must use the Pythagorean theorem to find this.
A perpendicular line dropped from the vertex to the 2-cm base will cut this base in half. This gives us 1 as one leg, an unknown leg, and 5 as the hypotenuse. The Pythagorean theorem states "the sum of the squares of the two legs of a right triangle equals the sum of the hypotenuse"; or, algebraically,
a² + b² = c²
Substituting our known information, we have
a² + 1² = 5²
a² + 1 = 25
Subtracting 1 from each side,
a²+ 1 - 1 = 25 - 1
a² = 24
Taking the square root of each side, we have
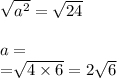
Using our formula for area, we have
A = 1/2(2)(2√6) = 1(2√6) = 2√6
Since we have two identical triangles, the combined area is
2(2√6) = 4√6
This makes the total cost
4√6(13.25) = $129.82