Hi!
I would approach this in a system of equations manner, when there are two equations, with two variables, and you solve for both. That's generally used when there are multiple conditional statements, like in this case, there are 2. (the sum is 61, larger is 15 more than smaller)
To do that, first assign your variables. To do that, figure out the things you are looking for. In this case, they are the numbers. So therefore:
Let l = larger number
s = smaller number
Now set up your two equations, with the two conditional statements.
The sum of two numbers is 61: l + s = 61, as you're adding the larger and smaller number to get 61.
The larger number is 15 more than the smaller number: 15 + s = l, as you have to add 15 to s, to get l, as l is larger.
Now set up your system.
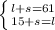
In this case I would use the substitution method, because we already have a variable defined, or l. To do substitution, in this case, you would take the l in the first equation, and set it equal to 15 + s, because from the second equation, you see 15 + s = l.
15 + s + s = 61
Now just solve for s.
2s = 46
s = 23
Now, you can just fill in s = 23 to any one of the previous equations, and then solve for l by isolating it. I'll just take the equation s + l = 61.
23 + l = 61
l = 38
There you have it, the numbers are 38 and 23.
If you want to check with the original equations (some math teachers say you have to,) just plug in the numbers into both original equations.
38 + 23 = 61: that is correct, so it works with The sum of two numbers is 61.
23 + 15 = 38: that is correct, so it works with The larger number is 15 more than the smaller number.
Hope this helped!