Question

A 15-ft ladder rests against a vertical wall. if the top of the ladder slides down the wall at a rate of 0.33 ft/sec, how fast, in ft/sec, is the bottom of the ladder sliding away from the wall, at the instant when the bottom of the ladder is 9 ft from the wall? answer with 2 decimal places. type your answer in the space below. if your answer is a number less than 1, place a leading "0" before the decimal point (ex: 0.35).

Answer 1

Let the corner of the wall and floor is our origin

Now the end of the ladder is on the floor is at distance x and top end on the wall is at distance y from this corner.

So we will use Pythagoras Theorem to find the length of the ladder.

`x^2 + y^2 = L^2`

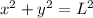
now if we differentiate whole equation with time

`2x(dx)/(dt) + 2y(dy)/(dt) = 0`

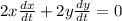
now the speed of the end of the ladder at the end of the floor will be given as

`(dx)/(dt) = -(y)/(x) (dy)/(dt)`

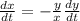
here
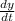`(dy)/(dt)` is the speed of end of the ladder on the wall.

so here we also know that

`9^2 + y^2 = 15^2`

`y = 12 ft`

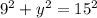
now we will plug in all values in the equation

`(dx)/(dt) = (12)/(9)*(0.33)ft/s`

`v = 0.44 ft/s`

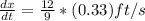
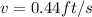
so the end of the ladder on the floor will move with speed v = 0.44 ft/s