Question

Which expression is equivalent to (4 + 7i)(3 + 4i)?. –16 + 37i

12 – 28i

16 – 37i

37 + 16i

Answer 1

`\text{Use:}\\(a+b)(c+d)=ac+ad+bc+bd\\i^2=-1\\-------------------------\\(4+7i)(3+4i)=(4)(3)+(4)(4i)+(7i)(3)+(7i)(4i)\\\\=12+16i+21i+28i^2=12+37i+28(-1)=12+37i-28\\=\boxed{-16+37i}`

Answer 2

ANSWER


`(4 + 7i)(3 + 4i) = - 16 + 37i`

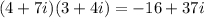
Step-by-step explanation

The given expression is

`(4 + 7i)(3 + 4i)`

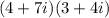
We need to expand the bracket using the distributive property as follows:


`(4 + 7i)(3 + 4i) = 4(3 + 4i) + 7i(3 + 4i)`

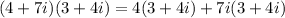
This implies that,


`(4 + 7i)(3 + 4i) = 4 * 3+ 4 * 4i+ 7i * 3 + 4i * 7i`

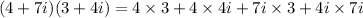
We simplify to obtain,


`(4 + 7i)(3 + 4i) = 12+ 16i+ 21i + 28 {i}^(2)`


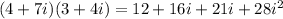
We now group like terms to obtain,


`(4 + 7i)(3 + 4i) = 12+ 37i+ 28 {i}^(2)`

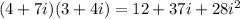
Now recall that

`{i}^(2) = - 1`

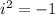
Applying this property gives,


`(4 + 7i)(3 + 4i) = 12+ 28 ( -1 )+ 37i`


`(4 + 7i)(3 + 4i) = 12 - 28+ 37i`


`(4 + 7i)(3 + 4i) = - 16 + 37i`

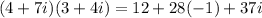
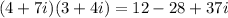
The correct answer is A.