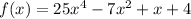Question

According to the Rational Root Theorem, -2/5 is a potential rational root of which function?

f(x) = 4x4 – 7x2 + x + 25

f(x) = 9x4 – 7x2 + x + 10

f(x) = 10x4 – 7x2 + x + 9

f(x) = 25x4 – 7x2 + x + 4

Answer 1

by the rational root theorem, the numerator of any possible rational root must be a factor of the constant term and the numerator must be a factor of the coefficient of the largest exponent term. the denominator of 5 means the leading coefficient must be a multiple of 5, which rules out the first two answers. the numerator of-2 required the constant to be even, so only the last answer is possible.
f(x)=25x⁴ - 7x² +x +4

Answer 2

According to the Rational Root Theorem, the possible roots can be found by taking ratios of the factors of constant term to the factors of leading coefficient

`f(x) = 4x^4 - 7x^2 + x + 25`

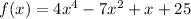
factors of constant 25 are 1, 5, 25

Factors of leading coefficient 4 are 1,2,4

We take + and - for all factors

Ratios are
`(+-1,5,25)/(+-1,2,4)`

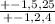
There is no -2/5 root

`f(x) = 25x^4 - 7x^2 + x + 4`

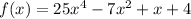
factors of constant 4 are 1,2,4

Factors of leading coefficient 25 are 1, 5, 25

We take + and - for all factors

Ratios are
`(+-1,2,4)/(+-1,5,25)`

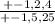
-2/5 is a potential rational root

Answer is
`f(x) = 25x^4 - 7x^2 + x + 4`