Question

Determine if the two functions f and g are inverses of each other algebraically. If not, why not?

f(x)=3/x-5 ; g(x)= 3+5x/x

A. No, ( f o g ) (x)= 3/5x-3
B. No, (f o g ) (x) =- 3/5x-3
C. Yes

Answer 1

The answer is C. "Yes."

Explanation:

Answer 2

The given functions are

`f(x) = (3)/(x-5) , g(x) = (3+5x)/(x)`

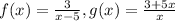
First we find fog(x)= f(g(x))

So we need to substitute the value of g(x) for x in f(x), that is

`f(g(x)) = (3)/((3+5x)/(x)-5) = (3x)/(3+5x-5x)`

`= (3x)/(3) = x`

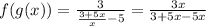
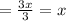
Now we need to check the value of gof(x)

gof(x) = g(f(x))

So we need to substitute the value of f(x) in g(x), that is

`g(f(x))=(3+5*(3)/(x-5))/((3)/(x-5))= (3x-15+15)/(3)`

`=(3x)/(3) = x`

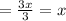
And since

`fog(x) =gof(x) =x`

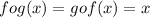
So the functions are inverse of each other .

Correct option is C .