Question

Please help me, thank you!!!

Answer 1

We need to find the probability that a selected animal will be an threatened given they are a bird: P(T/B). So,

`P(T/B)= (P(T\cap B))/(P(B))`

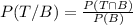
Where, Probability of threatened animal that are birds:

`P(T \cap B)` =
`(15)/(475)`

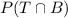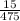
and probability of bird=
`(90)/(475)`

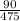
Therefore, P(T/B)= \frac{P(T\cap B)}{P(B)}

=
`((15)/(475))/((90)/(475))`

=
`(15)/(90)`

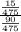
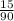
=0.1667

=16.67%