Question

The first number is eight more than the second one. Three times the second number plus twice the first number is equal to 26. Find the numbers

Answer 1

Let us consider the second number would be

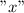
The first number is eight more than the second one.

That is, the first number would be " src="
`image`

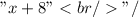
Three times the second number would be

Twice the first number would be

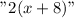
Now write the statement in mathematical form: "Three times the second number plus twice the first number is equal to 26"

`image`

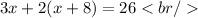
Solve this equation for x:

Distribute 2 in
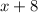`x+8`, we get

`3x+2x+16=26`

Combine the like terms,

`5x+16=26`

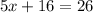
Subtracting 16 on both sides,

`5x+16-16=26-16`

`5x=10`

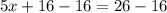
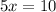
Dividing 5 on both sides,

`x=10/5=2`

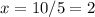
So the second number is
`x=2.`

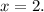
Now find the first number:

First number
`= x+8=2+8=10.`

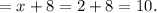
Thus the numbers are 10 and 2.