Question

Find the sum of a finite geometric series. The Smiths spent $2,000 on clothes in a particular year. If they increase the amount they spend on clothes by 10% each year, the Smiths will spend a total of $ on clothing in 4 years.

Answer 1

`\bf \stackrel{\textit{first year}}{2000}~~,~~\stackrel{\textit{second year}}{2000+\stackrel{\textit{10\% of 2000}}{(2000)/(10)}}\implies 2200`

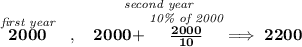
now, if we take 2000 to be the 100%, what is 2200? well, 2200 is just 100% + 10%, namely 110%, and if we change that percent format to a decimal, we simply divide it by 100, thus
`\bf 110\%\implies \cfrac{110}{100}\implies 1.1`.

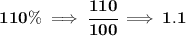so, 1.1 is the decimal number we multiply a term to get the next term, namely 1.1 is the common ratio.

`\bf \qquad \qquad \textit{sum of a finite geometric sequence}\\\\S_n=\sum\limits_(i=1)^(n)\ a_1\cdot r^(i-1)\implies S_n=a_1\left( \cfrac{1-r^n}{1-r} \right)\quad \begin{cases}n=n^(th)\ term\\a_1=\textit{first term's value}\\r=\textit{common ratio}\\----------\\a_1=2000\\r=1.1\\n=4\end{cases}\\\\\\S_4=2000\left[ \cfrac{1-(1.1)^4}{1-1.1} \right]\implies S_4=2000\left(\cfrac{-0.4641}{-0.1} \right)\\\\\\S_4=2000(4.641)\implies S_4=9282`