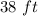Answer:
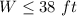
The maximum width must be
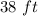
Explanation:
Let
L ----> the length of the rectangular pool
W ---> The width of the rectangular pool
we know that
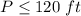
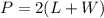
so
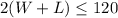 ----> inequality A
----> inequality A
we have
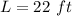
substitute the value of L in the inequality A
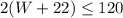
simplify
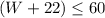
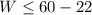
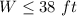
The maximum width must be