Question

Which of the following describes the function −x4 + 1? (6 points)

A. The degree of the function is even, so the ends of the graph continue in opposite directions. Because the leading coefficient is positive, the left side of the graph continues down the coordinate plane and the right side continues upward.

B. The degree of the function is even, so the ends of the graph continue in the same direction. Because the leading coefficient is negative, the left side of the graph continues down the coordinate plane and the right side also continues downward.

C. The degree of the function is even, so the ends of the graph continue in opposite directions. Because the leading coefficient is negative, the left side of the graph continues up the coordinate plane and the right side continues downward.

D. The degree of the function is even, so the ends of the graph continue in the same direction. Because the leading coefficient is positive, the left side of the graph continues up the coordinate plane and the right side also continues upward.

Answer 1

You have the equation:

`-x^(4)+1`

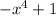
Therefore it has an even power and it has a leading negative coefficient.

An even power causes the ends of the graph to continue in the same direction, and the leading coefficient determines direction - if the coefficient is negative, the ends will be pointing downward, if the coefficient is positive, the ends will be pointing upward.

Therefore the correct answer is B) The degree of the function is even, so the ends of the graph continue in the same direction. Because the leading coefficient is negative, the left side of the graph continues down the coordinate plane and the right side also continues downward.