Question

Convert 4(cos(120)+i sin(120)) into rectangular form

A. (-4 ,4sqrt3)
B. (-2 ,2sqrt3)
C. (2sqrt3 ,-2)
D. (4 ,4sqrt2)

Answer 1

Try using polar expression forms. z = r(cos theta + sin theta) as well as x = r cos theta and y = r sin theta. Plug in the values you have. x = 4 cos 120 or 2pi/3 and solve. Do the same for y = 4 sin 120 or 2pi/3. It will give the "x" and "y" parts of your rectangular coordinates.

Answer 2

Option B
`(-2,2√(3))`

Explanation:

Given : Expression
`4(\cos(120)+i \sin(120))`

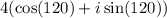
To find : Convert the expression into rectangular form?

Solution :

The rectangular form is
`a+ib`

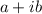
Now, We solve the expression

`4(\cos(120)+i \sin(120))`

`=4(\cos(90+30)+i \sin(90+30))`

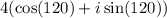
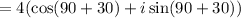
Applying trigonometric properties,

`\cos(90+\theta)=-\sin\theta\\\sin(90+\theta)=\cos\theta`

`=4(-\sin(30)+i \cos(30))`

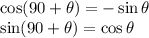
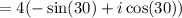
Substitute,
`\sin(30)=(1)/(2)\ , \cos\tehta (30)=(√(3))/(2)`

`=4(-(1)/(2)+i(√(3))/(2))`

`=-4* (1)/(2)+4* (√(3))/(2))i`

`=-2+2√(3)i`

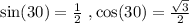
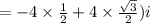
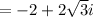
Therefore, The rectangular form is
`4(\cos(120)+i\sin(120))=-2+2√(3)i`

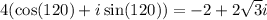
So, Option B is correct
`(-2,2√(3))`