Answer:
4.7935 days
Explanation:
The expression that describes exponential decay is the following:
N(t) = No *
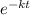
Where N(t) is the mass of the substance after a period t of time.
No is the original amount of substance
k is the relative decay rate and t is the period of time elapsed.
The half life is the period of time after which the amount of substance has decreased by half.
We can issolate t in the expression, using the properties of logarithms:
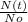 =
=
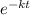
ln(
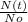 ) = -k*t
) = -k*t
t = - ln(
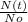 )/k = - ln(
)/k = - ln(
 )/0.1446 = 4.7935 days.
)/0.1446 = 4.7935 days.